Theory of mechanics:
The stated principle is purely mathematical and will have to use unconventional terms. This is the construction of a three-dimensional “matrix” with one and the same particle in motion. This imaginary particle is simply guided by an ultra-powerful imaginary field. This field allows the oscillatory movement of the particle from a point A to a point B for example. The advantage or the physical challenge would be to be able to see the human eye several points or particles at the same time, and in several different places. In cinematography, it takes just 24 frames per second to perceive and obtain seamless fluency in all types of contiguous, local and underlying movement. Based on the optical illusion, oscillating or alternating a particle of 5mm from a position A to a position B spaced by 10cm at the speed of light, would be seen as two visible points in the form of fixed and static appearance. The most important is to be able to mark a certain stop on each position of A and B, and to travel between it almost instantly.
I – Condition, particularity and foundation
What must be admitted in order to approve the following and the physical phenomenon: * The static state of the mass of a particle: Very high frequency back-and-forth movement of a single particle between the A and B positions, to give a static state of its mass at each point (admission visual).
– Immobility and movement of the particle between positions A and B:
1st fundamental condition of the stated principle and desired result of observation: The particle is either moving or stationary. No intermediate value is considered. If the particle is on A or B, then it is undeniably motionless. Only in its immobility the rotation of the particle itself is allowed. The movement represents the path to be traveled as quickly as possible between the positions of A and B (flow). In other words, only the distance traveled between A and B represents the movement of the particle, which is translated by the flow.
– Simulation of the almost instantaneous travel time of the particle between the A and B positions:
2nd fundamental condition of the stated principle and desired observation result: For reasons of efficiency and simplification of calculation, we can reduce the travel time of the particle between the positions of A and B to almost instantaneous value time. For example the particle can thus make the path from A to B to millions of billions of times the speed of light, to simply approach a possible symbolic value of zero seconds. We will speak rather of almost instantaneous value, expressed about zero seconds 0 ~ S (value and constant fictitious). It is also possible to exploit a reasonable value of the travel time which is far from zero seconds, for example:
Our big-bang = point A
Our sun = point B
Journey from A to B in 1 nanosecond (ns).
But the desired result of the journey time is about zero seconds. This is a mathematical exploitation of the almost infinite acceleration in terms of speed of displacement. It gives an extreme and considerable developed energy to move the particle at this speed. Example: E = mc². In absolute terms, and in terms of probability, we could say that the particle is on A or on B but never between the two (flow ~ 0s). In this case it is also possible to compare the flux with a bundle of high energy strings of very very low mass between A and B.
Mechanism and method of acceleration and deceleration of the particle between positions A and B: The particularity of the imaginary field CI which directs the particle, and to be able to accelerate to the square and / or to the cube and more, the speed of displacement of the particle between the positions A and B. For this to be consistent, and half-way, the particle must also decelerate to ² and more to anticipate the next stop stage, and arrive at destination to remain stationary and still for a moment.
– Increase and decrease the distance between positions A and B:
3rd fundamental condition of the stated principle and desired observation result: The travel time of the particle between the positions of A and B remains unchanged as the distance varies. In this case the position A remains fixed, and only the position B evolves in terms of distance in the space of the studied system. As the distance increases between A and B, the speed of movement increases, while the travel time remains unchanged between the two positions.
Later position A will become the origin point of the matrix, 4th foundation.
Example for a long travel time between positions A and B:
If the particle has to travel 10cm, it will travel from A to B in 1nS
If the particle has to travel 1Km, it will travel from A to B in 1nS
If the particle has to travel 10000Km it will travel from A to B in 1nS
Desired and expected result as a fictional constant:
If the particle has to travel 10cm, it will travel from A to B in ~ 0S
If the particle has to travel 1km, it will travel from A to B in ~ 0S
If the particle has to travel 10000Km it will travel from A to B in ~ 0S
II – Static density
The point of static density represents positions A and B for example. Reminder: Only the repeated high frequency alternation of the particle can give the appearance of static state of the mass between A and B.The principle described is a harmonic oscillator; but at very high frequency. The fixed static density is given at each end point of the particle, where between two the acceleration would be extremely high.
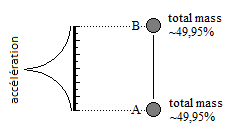
- Static mass density point and total mass density of the particle:
In order to be able to represent points of static density such as A and B at high frequency, it is first necessary to include the total mass density; The particle itself. In definition and in detail of the static density point: the static density point represents a total mass density part, and represents a zero mass part. This creates a paradox, because the static state of the particle requires two states (there and not there) of the particle on a position to be called static.
– Effective position and free position:
The effective position and the free position determine the characteristic and definition of the static density point. In other words, the static density point requires two states of positions to be defined as static. Effective and free (there and not there / paradox). At the point of static density: if the particle is on A then it is an effective position (total mass) and B becomes a free position (zero mass). And vice versa
Effective position = total mass = certain duration and formal presence of the particle without movement (rotation of itself admitted)
Free position = mass non-existent = certain duration of vacuum, but already was swept by the effective position
A free position is a position that has already been swept by the effective position. The free and effective positions determine the total size of the desired finite matrix. Positions outside the matrix become potential positions and embody the evolutionary and infinite matrices by expansion or incrementation of the original space.
– Potential position:
The potential position has never been swept by the effective position. Potential positions swept by the effective position become free positions. Positions of potential encompass all infinite points and represent a new and blank space, and constitute a form of emptiness. The flow can cross free positions and potential positions.
– Frequency and oscillation of the particle between positions A and B:
The amplitude represents the distance. The complete oscillation of the particle between the positions A and B represents a period in square analog signal (total stop on A and on B). A point of static density therefore requires two positions multiplied by a frequency. The rate of the frequency is given by the intrinsic frequency of the imaginary field CI which directs the particle. This dwell time defined by CI of the effective position, thus gives the duration of the particle on the position A and B for 1ns. If the frequency of the CI field is zero, then the density of the mass of the particle is not static.
(time position A + travel time to B + time position B + travel time to A) x frequency
(1ns + 0.0001ns + 1ns + 0.0001ns) x frequency
or
(1ns + ~ 0s + 1ns + ~ 0s) x frequency
For a high-frequency oscillation and the natural balance between A and B we have the example of a distribution of the total mass of the particle of:
49.995% for position A
49.995% for position B
0.01% for the flow (example of quantified flow)
Here is what would be visible to the human eye: two gray dots uniform at 49.995% of the black. (If we had to represent this particle without movement on a white background, then the 100% total mass particle would be a black dot.When the density of the total mass divides and moves in lower density, then this is represented by the shades of gray.)
III – Holographic Matrix
The term matrix used is out of context, and is there only to represent the shape of the structure, which is squared with points of static density.
point = dot

– Finite matrix 1 point, two positions:
4th fundamental condition of the stated principle and desired result of observation: Creation of a single point of static density, but in two positions; the stopping time of the second position being too short called point of origin.
The matrix one point two positions is formerly A and B, where A becomes the point of origin, and B the matrix point 1, except that here the downtime on the position A remains very short, while the time of stop is longer on position B.
Example of distribution of the granted time of the effective position of the system one point, two positions: Duration granted with the imaginary field CI which directs the particle:
(point of origin duration + amount flow duration + point matrix 1 duration + down flow duration) x frequency
(0.0001ns + ~ 0s + 1ns + ~ 0s) x frequency
Example of legend of the distribution of time granted from the effective position:
po = point of origin = 0.0001ns
–> = flow = ~ 0s
point1 = matrix point = 1ns
(po → point1 →) = cycle = ~ 1,0001 ns
cycle x frequency
Example of distribution of the total mass of the particle according to the time allowed of the effective position:
po = 0.000999% of total mass
→ = ~ 0% of total mass
point1 = 99.999% of total mass
To the human eye we would see a single point at ~ 99.9% of the black with one particle, but in two positions.
– Point of origin :
The point of origin always lists the starting point, and the zero position of the matrix system. The point of origin is not a matrix point, and is excluded from the matrix. It is therefore separated from the matrix by the flow which is up and down (flow dynamics). The point of origin is a point of static density in its own right, because the particle marks a total and certain stop. This stop in the effective position is as short as possible, and especially shorter than the matrix points which are them in longer stop. The point of origin represents the source and database of the matrix bound by the particle in the flow. The addressing of the particle by the point of origin makes it possible to assign the information and the resource for the next static point to be created in the matrix: (direction, distance, duration of the effective position, polarity, susceptibility, speed of rotation, flavor). The point of origin also represents the lowest alternation of the CI field occupied by the system, the matrix being the different high alternations. At each peak of collapse of the CI wave function, determines the access to the point of origin.
– Compensation of mass and point of origin:
In order to distribute the total mass in the matrix in a controlled manner, the point of origin can also absorb and compensate for the duration of the effective position. Example: if we want a matrix point of 10% of total mass for a matrix one point two positions, the point of origin must absorb 90% of total mass with the duration of the effective position. In this case the point of origin would be visible, but it does not count as a matrix point.
– Scanning of the effective position, and total refresh of the finite space of the free positions:
cycle = Refresh all free positions of the finished matrix by the effective position, based on the point of origin (point-to-point). Each point that is created, or projected into the matrix by the effective position, automatically returns to the point of origin. The cycle counts for an intrinsic time unit. If a cycle lasts 1ns, then the intrinsic time value will be 1. If a cycle lasts 250ns, then the intrinsic time value will also be 1. This unit asserts the total refresh number of the matrix, and is the first image (stop motion). This refresh is endowed with no intrinsic motion, because the intrinsic motion is due to the displacement of the densities after several cycles. The intrinsic distance lies between the matrix points themselves, and not between the point of origin and the matrix.
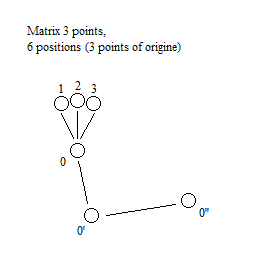
– Matrix finished 3 points 4 positions:
Example of distribution of the granted time of the effective position of the system 3 points, 4 positions:
Duration granted with the imaginary field CI which directs the particle:
po = point of origin = 0.0001ns
–> = flow = ~ 0s
point(n) = matrix point = 1ns
(po → point1 → po → point2 → po → point3 → ) = cycle ~3,0003ns
cycle x frequency
Example of distribution of the total mass of the particle of the system 3 points, 4 positions:
Example of distribution of the total unit mass per shift:
po = 0.00033%
→ = ~ 0%
point(n) = 33,333%
(po → point1 → po → point2 → po → point3 → ) x frequency
(3 x po) + (6 x → ) + (3 x point)
(0.00099%) + (~ 0%) + (99.999%)
To the human eye we would see three gray spots at ~ 33.3% of the black.
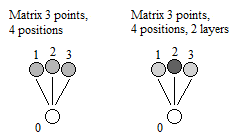
– Superposition of layers of static mass density, and weight:
Repeated several times with the effective position in the same free position at the expense of other free positions for a cycle. As for our atoms we have a maximum weight limit. For some coherent finite matrices we have the assumed example of 10 maximum layers. These layers can represent elements (element 1 layer, element 2 layers, …).
Weight = number of superposed static density layers, one position, one cycle
Example:
Matrix 3 points, 4 positions, 2 layers:
This matrix thus comprises 3 matrix points with the passage of the effective position for each of the points, and 2 additional ironings of the effective position on only one of the three points, for one cycle. One layer counts for one additional density point. Example:
Time allocation of effective position:
(po → point1 → po → point2 → po → point2 → po → point2 → po → point3 → ) = cycle = ~ 5ns
cycle x frequency
Let the example of about 1ns per position:
point1 = ~ 1ns
point2 = ~ 3ns
point3 = ~ 1ns
Example of distribution of the total unit mass per shift:
For this example the flow is quantized, and is different from ~ 0%.
po = 0.000999% for the point of origin
–> = 0.000001% for the flow
point (n) = 19.998999% for the matrix
(po → point1 → po → point2 → po → point2 → po → point2 → po → point3 → ) x frequency
(5 x po) + (10 x –>) + (5 x point)
po = 0.000999% x 5 = 0.004995%
→ = 0.000001% x 10 = 0.00001%
point1 = 19.998999% x 1 = 19.998999%
point2 = 19.998999% x 3 = 59.996997%
point3 = 19.998999% x 1 = 19.998999%
To the human eye we would see three points, only one more visible than the other two.
– Transfer of superposed layers of static density:
This movement is said to be intrinsic because it represents the change of position of superimposed density layers during the transition from one cycle to another. Example:
Matrix 3 points, 4 positions, 2 layers:
Displacement and transition of heavy static density from point 2 to point 3:
(po–>point1–>po–>point2–>po–>point2–>po–>point2–>po–>point3–>) = cycle1 = intrinsic motion 0
(po–>point1–>po–>point2–>po–>point3–>po–>point3–>po–>point3–>) = cycle2 = intrinsic motion 1
Moving layers by flashing between points 2 and 3:
(cycle1 + cycle2) x frequency
This blinking is too fast to be seen with the human eye Transfer layers by flashing twice as fast:
(cycle1 + cycle2 + cycle2 + cycle1) x frequency
– Increase the density of the total mass of the particle without changing the size of the particle:
The mathematical advantage is to be able to increase the mass of a small particle without changing its size. This principle is reminiscent of neutron stars. For example one could say that some milli-cube of material could weigh several tons. The advantage is the construction of a larger matrix with a small amount of mass very heavy in terms of density. Direct ratio between matrix sizes and total mass density of the particle.
Black contrast level in relation to the total mass of the particle:
1,000,000% = contrast: black = weight: very heavy
1000% = contrast: black = weight: heavy
100% = contrast: black = weight: normal maximum
1% = contrast: gray 1% = weight: normal low
– Matrix 257 points, 258 positions, 190 layers (10×19):
Example of a partial spherical matrix, with a total density of 10,000%, and a cycle time of about 448 ns:

- Spherical matrix and cubic matrix (3 dimensions):
Example of a semi-cubic matrix display structure
(po–>point1–>po–>point2–>po–>point3–>po–>point4–>) = line1
(po–>point5–>po–>point6–>po–>point7–>po–>point8–>) = line2
(po–>point9–>po–>point10–>po–>point11–>po–>point12–>) = line3
(po–>point13–>po–>point14–>po–>point15–>po–>point16–>) = line4
(line1 + line2 + line3 + line4) = block1 = square surface
(po–>point17–>po–>point18–>po–>point19–>po–>point20–>) = line5
(po–>point21–>po–>point22–>po–>point23–>po–>point24–>) = line6
(po–>point25–>po–>point26–>po–>point27–>po–>point28–>) = line7
(po–>point29–>po–>point30–>po–>point31–>po–>point32–>) = line8
(line5 + line6 + line7 + line8) = block2 = square area = top slice 1
(block1 + block2) = semi-cubic surface of 4 x 4 X 2
(block1 + block2) = cycle = ~ 32,0032ns
cycle x frequency
- Total or partial spherical matrix:
Making a clock on the upper floors of a spherical matrix, will be formed less quickly than on the lower floors of the same matrix. This is an intrinsic time dilation for a single cycle, even though the actual duration of this cycle remains unchanged. On spherical matrices we have an optimum matrix layer; a cruising active surface, because the alignment of the matrix points is more favorable.
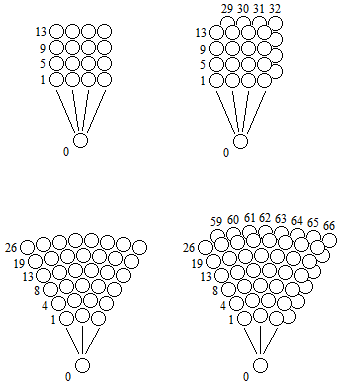
– Infinite matrix:
Progressive infinite matrix starting from a matrix one point, two positions:
Incrementation possible to enlarge the finite matrix to infinity:
(po–>point1–>) = cycle1
(po–>point1–>po–>point2–>) = cycle2
(po–>point1–>po–>point2–>po–>point3–>) = cycle3
(po–>point1–>po–>point2–>po–>point3–>po–>point4–>) = cycle4
The actual duration of the cycle is extended, because for example the display of the point1 is delayed at each cycle refresh. In reality it is false for the object that is formed that does not see itself slow down.
(cycle1) = 1,001ns = intrinsic time: 0
(cycle2) = 2.002ns = intrinsic time: 1
(cycle3) = 3,003ns = intrinsic time: 2
(cycle4) = 4.004ns = intrinsic time: 3
For the matrices ends the actual duration of the cycle remains the same, since the finite matrices are definitively determined by a number of known and fixed matrix points. Adding a matrix point comes down to slowing the real time of the cycle time. In the case of a total exploitation of the total mass, an already equilibrium matrix can no longer accommodate an additional density point, since the latter depletes and alters all the superimposed elements and objects. The transformation will be done by favoring a different distribution of the same values, even within superimposed densities. It is therefore difficult to add or remove the mass to a matrix already in equilibrium, unless the compensation of the mass is important at the point of origin.
- Linear incrementation of the total mass density of the particle:
Corresponds to the simple displacement of the particle in a straight line, where is conserved 99.9% of its total mass. Simulation of the rectilinear displacement of an point-to-point particle from its po source:
(po–>point1–>) = cycle1 = display position 1 = 99.9% mass = intrinsic motion 0
(po–>point2–>) = cycle2 = display position 2 = 99.9% mass = intrinsic motion 1
(po–>point3–>) = cycle3 = display position 3 = 99.9% mass = intrinsic motion 2
– Concentric circular distribution of fixed total mass density of the particle:
This concentric circular expansion is similar to the distribution of light density, where the static mass density decreases as the wave propagates (longer circumference length to irrigate).
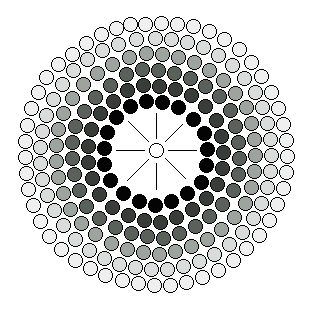
– Concentric circular distribution of variable total mass density of the particle:
Adjustment of the total mass in relation to the circular expansion density.
– Double matrix with a single point of origin:
Double or triple matrices and more, are simply separated by positions of potential not scanned by the effective position.

– Added a 2nd “lower” origin point with the same particle (same system):
Example with a matrix 3 points, 5 positions:
Time allocation of effective position:
(po2–>po1–>point1–>po1–>po2–>po1–>ponit2–>po1–>po2–>po1–>point3–>po1–>)
Adding a second point of origin is very easy. It is enough to add an additional crossing position on the low alternation of CI. This second point of origin is also a very short effective position. Example: without changing the speed of refresh cycle: amputate time on the already existing point of origin; If the duration of the effective position on the point of origin is 0.1ns, then creating a second point of origin could be 0.05ns for po1, and 0.05ns for po2. Triple system and more possible.
– Double system:
The double system is a single matrix built with two particles, including two commutative origin points. Example with the compensation of the mass at the point of origin: If the particle n° 1 is on its point of origin as effective position, then the matrix is free; So particle n° 2 will be represented in the matrix as the effective position and will have its point of origin in free position. The final crossed and interfered matrix may become denser if both particles are at the same time in the matrix as the effective position, constituting a single mixed matrix. Triple system and more possible.